Möbius-Band mit Tinkercad Codeblocks

Entdecke, wie du mit Tinkercad Codeblocks ein Möbius-Band aus 360 Quadern erstellst. Ideal für alle, die Geometrie kreativ umsetzen möchten!

Was brauchst du?

Schritt 1: Was ist ein Möbius-Band?

Ein Möbius-Band ist eine Fläche mit nur einer Seite und einer Kante. Man erhält es, wenn man einen Papierstreifen nimmt, ihn einmal um 180 Grad verdreht und die Enden zusammenklebt.

Das Besondere daran: Wenn man mit einem Stift eine Linie auf der Oberfläche zieht, landet man – ohne den Stift abzusetzen – wieder am Ausgangspunkt, aber auf der „anderen Seite“ des Bandes. Es ist ein klassisches Beispiel für eine nicht-orientierbare Fläche – und ein Liebling unter Mathematikbegeisterten.

Schritt 2: Der Grundgedanke

Die Herausforderung beim Nachbauen eines Möbius-Bandes in einem 3D-Modell besteht darin, diese kontinuierliche Verdrehung mathematisch zu beschreiben und in einzelne Bausteine zu übersetzen.

Ich habe mich dazu entschieden, das Band aus vielen kleinen Quadern aufzubauen, die in einem bestimmten Muster im Raum positioniert und verdreht werden. Jeder Quader steht dabei für einen kleinen Abschnitt des Bandes. Durch Rotation und Verschiebung entsteht am Ende der typische Möbius-Effekt.

Schritt 3: Umsetzung mit Tinkercad Codeblocks

Tinkercad Codeblocks ist eine tolle Umgebung, um Geometrie mit einfachen Programmierkonzepten zu verbinden. So bin ich vorgegangen:

1. Wiederholungsschleife von i = 1 bis 360:
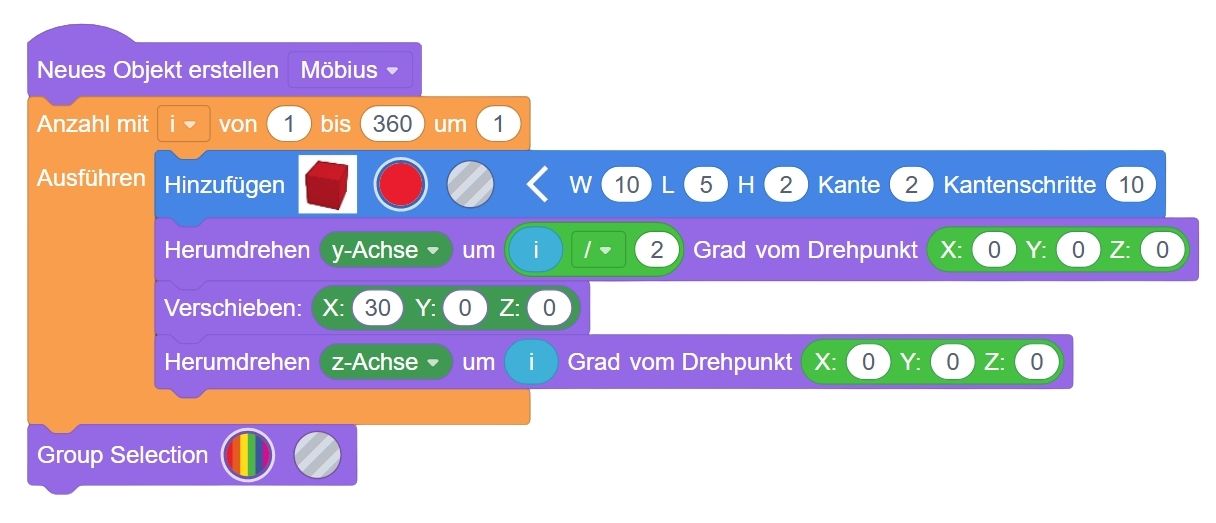
   Ich erstelle insgesamt 360 Quader – jeder entspricht einem kleinen Teilstück des Möbius-Bandes.
2. Quader erstellen:
   Jeder Quader hat abgerundete Ecken, damit das Ganze etwas weicher wirkt.
3. Rotation um sich selbst:
   Jeder Quader wird um i / 2 Grad um seine eigene Y-Achse gedreht – das erzeugt die Verdrehung des Bandes.
4. Verschiebung in X-Richtung:
   Danach wird der Quader um 30 Einheiten in X-Richtung verschoben – damit bildet sich eine Kreisbahn um den Mittelpunkt.
5. Rotation um den Mittelpunkt:
   Zuletzt wird der Quader um i Grad um die Z-Achse des Modells gedreht – das legt die Quader im Kreis an.

Das Ergebnis ist ein spiralförmig verdrehtes Band – kein perfektes mathematisches Möbius-Band, aber eine überraschend schöne Annäherung, die mit den Bordmitteln von Tinkercad gut funktioniert.

Fazit

Mit Tinkercad kann man tolle und auch mathematisch interessante Designs und Objekte erstellen! Ein Möbiusband ist nur eine mögliche Idee. Hier findest du weitere Ideen mit Tinkercad!